Дан треугольник ABC с ортоцентром H. В него вписана окружность с центром в точке I, которая касается сторон BC, AC, AB в точках A_1, B_1, C_1 соответственно. Прямые A_1H и AI пересекаются в точке A_2. Аналогично определим точки B_2 и C_2. Докажите, что ортоцентр треугольника A_2B_2C_2 совпадает с H.

На плоскости нарисовано m синих и n красных окружностей, при этом любые окружности разных цветов касаются, а одинакового цвета - нет. Могут ли m и n быть равны a) 3 и 8; b) 3 и 9; c) 4 и 6; d) 4 и 7?

P.S. Выше картина В. Кандинского "Несколько кругов" 1926 г.

Дан треугольник ABC. В него вписана окружность с центром в точке I. К ней провели касательную, которая параллельна BC и выбрали на этой касательной точки U и V такие, что угол UIV = 90. Прямые IU и IV повторно пересекают окружность (AUV) в точках P и Q. Докажите, что точки O, P, Q лежат на одной прямой, где O — центр описанной окружности треугольника ABC.

Обобщение теоремы Паскаля. Цветные фигуры — эллипсы.

добавлю к предыдущему утверждению вот какой контекст

на картинке (взятой у Мат. этюдов) — теорема Монжа (вот, кстати, еще подборка доказательств)

можно ли заменить в ней окружности на эллипсы? на произвольные нельзя, но можно — на эллипсы с общим фокусом

как и в многих других утверждениях, вместо фокуса можно рассматривать обобщенный фокус — окружность, дважды касающуюся эллипса (настоящий фокус получается, когда радиус этой окружности нулевой — это не так заметно, потому что точки касания при этом становятся комплексными)

вот такой родственник теоремы Монжа и нарисован на предыдущей картинке

upd: можно еще сказать, что это — гиперболическая версия теоремы Монжа (нарисованная в модели Клейна)

Задачи с турнира

В июне этого года прошел турнир имени Савина для школьников 7 и 8 классов. На нем ребята решали несколько моих задач. Предлагаю вам подумать над двумя из них.
Просьба: в комментах пишите только свои ответы:)

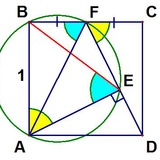
20 теорем об углах в треугольнике и не только

Увидел в ФБ такую вот коллекцию. Большая часть кажется весьма полезной, хотя и редко употребительной. Какие из «не школьной» части этого списка вы считаете самыми ценными?